Question

8 yd10 yd|Which is the lateral area for the cylinder?48760719671207

Answer 1

We must compute the lateral area of the cylinder of the figure.

From the figure we see that the cylinder has:

• a height h = 8 yd,

,

• the inner right triangle with hypotenuse H = 10 yd.

To find the lateral area we need the diameter d of the cylinder. From the picture we see that the diameter of the cylinder is one of the cathetus of the inner right triangle:

Using Pythagoras Theorem we compute the diameter of the cylinder:

`\begin{gathered} H^2=d^2+h^2 \\ d^2=H^2-h^2 \\ d=\sqrt[]{H^2-h^2} \\ d=\sqrt[]{(10yd)^2-(8yd)^2} \\ d=\sqrt[]{36yd^2} \\ d=6yd \end{gathered}`

Now, the lateral area of the cylinder can be computed by multiplying the longitude of the circumference of the cylinder (which is π*d) and the height (h). We find that the lateral area of the cylinder is:

`\begin{gathered} A=(\pi\cdot d)\cdot h \\ A=(\pi\cdot6yd)\cdot8yd \\ A=48\pi\cdot yd^2 \end{gathered}`

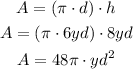
Answer

48π