Question

A study is done on the number of bacteria cells in a petri dish. Suppose that the population size after hours is given by the following exponential function.

Answer 1

Given the exponential function:

`P(t)=1800(1.03)^t`

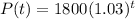
Where P models the population size after t hours. The initial population size can be obtained using t = 0:

`\begin{gathered} P(0)=1800(1.03)^0=1800(1) \\ \therefore P(0)=1800 \end{gathered}`

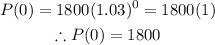
The initial population size is 1800.

Now, since the term inside the parentheses is greater than 1, we can conclude that this function represents a growth tendency.

Finally, we can take the ratio between the population size at time t and at time t+1:

`\begin{gathered} (P\left(t+1\right))/(P(t))=(1800(1.03)^(t+1))/(1800(1.03)t)=1.03=1+0.03 \\ \\ Change:\Delta=|1-(P(t+1))/(P(t))|=|1-1-0.03|=0.03 \end{gathered}`

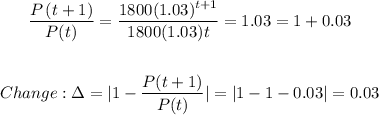
In percent form, the change is 3%