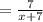Question

Pictures sent I solved problem and would like toKnowIf I did it correctly

Answer 1

Step-by-step explanation

Since we have the expression:

`(7x+42)/(x^2+13x+42)`

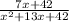
Factoring 7x + 42:

`\mathrm{Rewrite\:}42\mathrm{\:as\:}7\cdot \:6`
`=7x+7\cdot \:6`

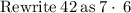
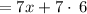
Factor out common term 7:

`=7\left(x+6\right)`
`=(7\left(x+6\right))/(x^2+13x+42)`

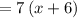
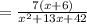
Factor x^2+13x+42:

Breaking the expression into groups:

`=\left(x^2+6x\right)+\left(7x+42\right)`

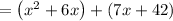
Factor out x from x^2+6x:

`=x\left(x+6\right)`

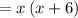
Factor out 7 from 7x + 42:

`=x\left(x+6\right)+7\left(x+6\right)`

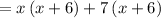
Factor out common term x+6:

`=(7\left(x+6\right))/(\left(x+6\right)\left(x+7\right))`
`\mathrm{Cancel\:the\:common\:factor:}\:x+6`

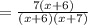
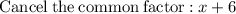
The final expression is as follows:

`=(7)/(x+7)`