Answer: This problem can be solved using the concept of mathematical proportions, the equation that can be constructed for the problem is as follows:

Solving equation (1) gives the answer, the solution to the equation (1) is as follows:
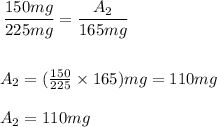
Therefore the answer is 110mg.