Question

Hi, can you help me answer this question please, thank you

Answer 1

3)

Assuming that the population of the study has a normal distribution and that you are studying the population mean μ.

The statistic hypotheses are

`\begin{gathered} H_0\colon\mu=87.8 \\ H_1\colon\mu<87.8 \end{gathered}`

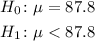
If you look at the alternative hypotheses, it includes the symbol "<", which indicates that the test is one-tailed. This means that you will reject the null hypotheses at small values of the test statistic.

Since the sample size is small (n=4) and the given sample data. The test statistic to use for the test is the Student's t:

`t=\frac{\bar{X}-\mu}{\frac{S}{\sqrt[]{n}}}\sim t_(n-1)`

To calculate the value of the statistic under the null hypothesis you have to use the sample data and the value of the population mean under the null hypothesis:

μ= 87.8

sample mean= 75

sample standard deviation= 17.1

n=4

`\begin{gathered} t_(H0)=\frac{75-87.8}{\frac{17.1}{\sqrt[]{4}}} \\ t_(H0)=(-12.8)/(8.55) \\ t_(H0)=-1.497 \end{gathered}`

The test statistic under the null hypothesis is -1.497

The p-value is the probability corresponding to the calculated statistic if possible under the null hypothesis.

So you have to calculate the probability of obtaining the value t=-1497

The student t has n-1 degrees of freedom, since the sample taken is n=4, the degree of freedom is 3.

The p-value is then the accumulated probability up to -1.497 under a t-distribution with 3 degrees of freedom:

`p-\text{value}=P(t_3\leq-1497)=0.115653\approx0.1157`

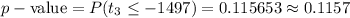
The p-value is equal to 0.1157

4)

To make a decision using the p-value, you have to compare the said value with the level of significance, following the decision rule:

- If the p-value ≥ α, do not reject the null hypothesis.

- If the p-value < α, reject the null hypothesis.

The p-value (0.1157) is greater than the significance level (α= 0.05)

The decision is "do not reject the null hypothesis."