SOLUTION
Write out the function
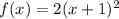
To find the equation of the line tangent of this function, we different the function to obtain the slope.
Expanding the function we have
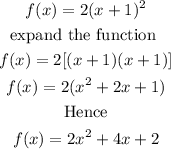
Apply the differebtiation rule, we have

hence, at the point (-2,2), the slope will be
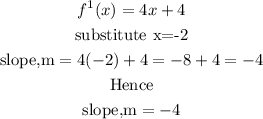
Then
Apply the Point- slope form for the equation of a line at point (-2,2)
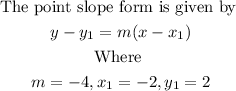
Substituting the value, we have

Exapand the paranthesis, and write the equation
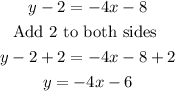
Hence
The equation of the line of tangent to the function is
y=4x-6 or y+4x= -6