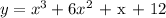Given point : (-5, 32)
A linear function would take the form:
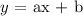
Substituting the given point:
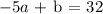
Our goal is to find the constants a and b.
set a = -5
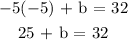
Solving for b:
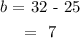
Hence, the linear equation:
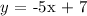
A quadratic function would take the form:
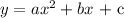
Substituting the given point:
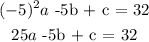
Set a = 1 and b = -1:
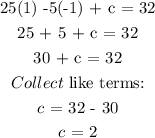
Hence, the quadratic equation is:
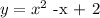
A cubic equation would take the form:
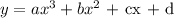
Substituting the given point:
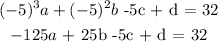
Set a = 1, b = 6, c = 1 :
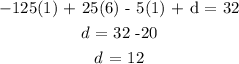
Hence, the cubic equation would be: