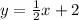Question

Write an equation of the line perpendicularto the given line that contains P.P (4, 4): y = -2x-8

Answer 1

For this problem we want to find the equation of a line perpendicular to the line y=-2x-8 and passing through the point (4,4). We can see that the slope for the line given is m1=-2 and since we want a perpendicular line we need to satisfy the following:

`m_1\cdot m_2=-1`

And solving for m2 we got:

`m_2=-(1)/(m_1)=-(1)/(-2)=(1)/(2)`

And then with the point given we can find the intercept:

`4=(1)/(2)(4)+b`
`b=4-2=2`

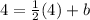
And the equation for the line would be:

`y=(1)/(2)x+2`