For this problem, we were given a certain dataset, as well as the quartiles Q1, Q, and Q3. From this information, we need to determine the lower and upper fences.
The fences are given by:
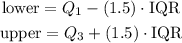
Therefore, we need to calculate the value of the IQR, which is the subtraction between Q3 and Q1.
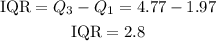
With this, we have all the data to determine the lower and upper fences. The calculations are shown below:
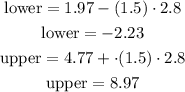
Since there aren't any values that are lower than the lower fence or higher than the upper fence, we don't have any outlier on this data.