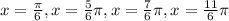Question

Solve the following trigonometric equation on the interval [0, 2π]12sin2x−3=0

Answer 1

Given the expression:

`12sin^2(x)-3=0`

To solve the expression, follow the steps below:

Step 01: Add 3 to both sides.

`\begin{gathered} 12sin^2(x)-3+3=0+3 \\ 12sin^2(x)=3 \end{gathered}`

Step 02: Divide both sides by 12.

`\begin{gathered} (12sin^2(x))/(12)=(3)/(12) \\ sin^2(x)=(1)/(4) \end{gathered}`

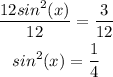
Step 03: Take the square root of both sides.

`\begin{gathered} √(sin^2(x))=\pm\sqrt{(1)/(4)} \\ sin(x)=\pm(1)/(2) \end{gathered}`

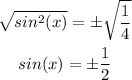
Step 04: Evaluate the results.

First, let's evaluate sin(x) = 1/2.

Sin(x) is positive in the first and in the second quadrant. Then,

`\begin{gathered} sin^(-1)((1)/(2))=x \\ x=(\pi)/(6),x=(5)/(6)\pi \end{gathered}`

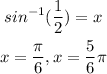
Second, let's evaluate sin(x) = -1/2.

Sin(x) is negative in the third and in fourth quadrant. Then,

`\begin{gathered} sin^(-1)(-(1)/(2))=x \\ x=(7)/(6)\pi,x=(11)/(6)\pi \end{gathered}`

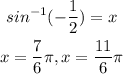
Answer:

`x=(\pi)/(6),x=(5)/(6)\pi,x=(7)/(6)\pi,x=(11)/(6)\pi`