ANSWER
35.7 m³
Step-by-step explanation
By the ideal gases law,
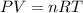
If we have the same gas in both situations, the product nR is constant, thus for this problem,
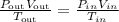
The given information is:
• Pout = 8500 Pa
,
• Pin = 2000 Pa
,
• Tout = 10 °C
,
• Tin = 35 °C
,
• Vout = 2.4 m³
,
• Vin =?
We have to solve the equation above for Vin,
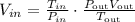
Replace the values,
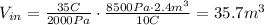
The new volume of the gas is 35.7 m³