As we know, the type of function that can be used to modelate populations is the exponential function, which, in our case will look like the following:
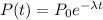
Where P0 is the initial population, and lambda is a parameter which tells us how fast the population decays. By replacing the values we have, we get:
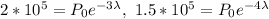
In order to find out the first parameter, let us divide both equations:

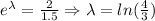
With this, we can find out the initial population by replacing lambda on any equation:
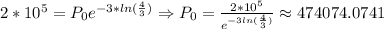
Thus, the population when t=10 will be approximately:
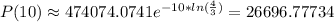
Thus, our answer is P(10)=26697