Question

Walking across a bridge, a tourist throws a penny into the water below. The penny’s height above the water in meters, p(x), depends on the time in seconds after throwing, x, and can be modeled with the function p(x) = -16x2+ 7x + 15. Approximately how many seconds after being thrown will the penny hit the water?

Answer 1

The given equation models the height of the penny p(x) with respect to the time x after being thrown from a bridge.

`p(x)=-16x^2+7x+15`

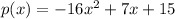
This equation is a quadratic equation, where the vertex represents the height where the "height of the bridge" where the coin was thrown from, and the right x-intercept represents the time it takes the coin to reach the water.

To determine the time it takes the coin to hit the water, you have to find the zeros of the quadratic expression. For this, you have to apply the quadratic equation:

`x=(-b\pm√(b^2-4ac))/(2a)`

Where

a is the coefficient of the quadratic term

b is the coefficient of the x-term

c is the constant of the quadratic expression

Considering the given equation, the coefficients are:

a= -16

b= 7

c= 15

Replace these values on the equation:

`\begin{gathered} x=(-b\pm√(b^2-4ac))/(2a) \\ x=(-7\pm√((7)^2-4*(-16)*15))/(2*(-16)) \\ x=(-7\pm√(49+960))/(-32) \\ x=(-7\pm√(1009))/(-32) \end{gathered}`

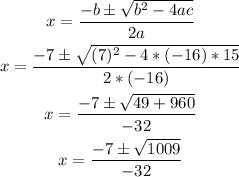
Calculate the sum and difference separately to determine the zeros of the equation:

-Sum:

`\begin{gathered} x=(-7+√(1009))/(-32) \\ x=-0.77 \end{gathered}`

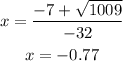
-Difference:

`\begin{gathered} x=(-7-√(1009))/(-32) \\ x=1.21 \end{gathered}`

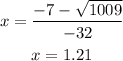
The left zero of the equation is x=-0.77s.

The right zero of the equation is x=1.21s.

As mentioned before, the time it takes the coin to reach the water is represented by the right zero of the quadratic equation.

This means that it takes 1.21 seconds for the coin to reach the water.