the sides of the quadrilateral WXYZ are NOT parallel
Step-by-step explanation
two segments are parallel if the slope is the same .so
the slope of a line ( or segment) is given by

Step 1
so, let's find the slopes of the sides
a)WX
let
W=P1(-1,-1)
X=P2(-3,-1)
now, replace in the formula
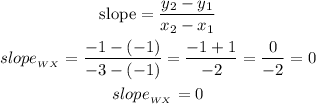
b)XY
let
X=P1(-3,-1)
Y=P2(-2,4)
now, replace in the formula
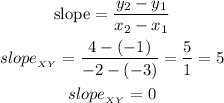
c)YZ
let
Y=P1(-2,4)
Z=P2(2,3)
now, replace in the formula

d)ZW
let
Z=P1(2,3)
W=P2(-1,-1)
now, replace in the formula
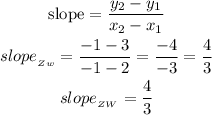
conclusion: two lines ( or segments are parellale if the slope is the same), here we found that the 4 slopes are differentes, so the sides of the quadrilateral WXYZ are NOT parallel
I hope this helps you