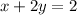Answer:
The equation in slope-intercept form will be;
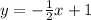
The function in point-slope form is;
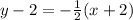
The standard form of the equation is;
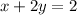
Step-by-step explanation:
Given the function f(x);
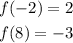
Firstly, let us find the slope;
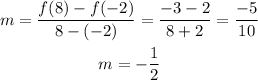
we can then solve for the constant term;
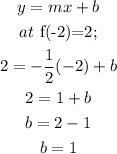
The equation in slope-intercept form will be;
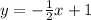
Applying the point-slope form of equation;
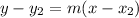
Substituting the second point;
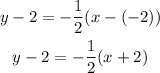
The function in point-slope form is;
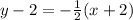
The standard form of the equation can be written as;
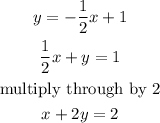
The standard form of the equation is;