Question

I need help can someone help me with the geometry question?

Answer 1

We are given the coordinates of the vertices of a quadrilateral. When we plot the points we notice the following figure:

Now, we will prove that this figure is a rectangle. First, for the figure to be a rectangle we need to prove that opposite segments are parallel, this means that their slopes are equal.

First, to determine the slope of a line segment we use the following formula:

`m=(y_2-y_1)/(x_2-x_1)`

Where:

`\begin{gathered} (x_1,y_1) \\ (x_2,y_2) \end{gathered}`

Are points in the segment.

First, we will determine the slope of the segment that has endpoints (-1,3) and (-5,-3), this means that:

`\begin{gathered} (x_1,y_1)=(-1,3) \\ (x_2,y_2)=(-5,-3) \end{gathered}`

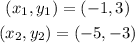
Substituting in the formula for the slope we get:

`m=(-3-3)/(-5-(-1))`

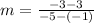
Solving the operations:

`m=-(6)/(-4)=(3)/(2)`

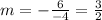
Now we will determine the slope of the side opposite to this. The end-points are:

`\begin{gathered} (x_1,y_1)=(2,1) \\ (x_2,y_2)=(-2,-5) \\ \end{gathered}`

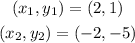
Substituting in the formula for the slope we get:

`m=(-5-1)/(-2-2)=-(6)/(-4)=(3)/(2)`

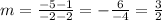
Since the slopes are both equal to 3/2, this means that the lines are parallel.

Now we determine the slope of the line with end-points (-1,3) and (2,1). This means:

`\begin{gathered} (x_1,y_1)=(-1,3) \\ (x_2,y_2)=(2,1) \\ \end{gathered}`

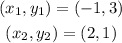
Substituting in the formula for the slope we get:

`m=(1-3)/(2-(-1))=-(2)/(3)`

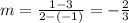
Now we use the segment in front of this one, we have the end-points:

`\begin{gathered} (x_1,y_1)=(-2,-5) \\ (x_2,y_2)=(-5,-3) \end{gathered}`

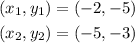
Now, we substitute in the formula for the slope:

`m=(-3-(-5))/(-5-(-2))=(2)/(-3)=-(2)/(3)`

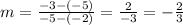
Since the slopes are the same this means that pairs of opposite sides are parallel.

Now we will prove that pairs of adjacent sides are perpendicular. They are perpendicular if the product of their slopes is -1.

Since pairs of opposite sides have the same slope It will be enough to prove that the product of the different slopes we found is euqal to -1. The first slope we determine is:

`m_1=(3)/(2)`

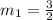
And the third slope we found is:

`m_2=-(2)/(3)`

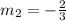
Now we determine their product:

`m_1m_2=((3)/(2))(-(2)/(3))=-1`

Since the product is -1, this means that adjacent sides are perpendicular and therefore, we have proved that the figure is a rectangle.