Question

1. Solve the problem.A person is watching a boat from the top of a lighthouse. The angle of depression from the person to the boat is 28°. The lighthouse is 200 feet tall. How far away is thelighthouse? Round to the nearest foot.

Answer 1

Given:

Description of a person's view from a lighthouse to a boat.

This can be sketched as shown below;

The sketch can be made as a right triangle;

To get the distance between the boat and the lighthouse, we use the trigonometrical ratio of tangent.

`\begin{gathered} \tan \theta=\frac{\text{opposite}}{adjacent} \\ \text{where;} \\ \theta=28^0 \\ \text{opposite=200} \\ \text{adjacent}=x \end{gathered}`

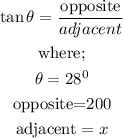
Hence,

`\begin{gathered} \tan \theta=\frac{\text{opposite}}{adjacent} \\ \tan 28=(200)/(x) \\ \text{Cross multiplying;} \\ x*\tan 28=200 \\ x=(200)/(\tan 28) \\ x=376.15 \\ To\text{ the nearest foot,} \\ x\approx376ft \end{gathered}`

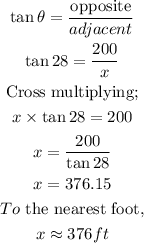
Therefore, to the nearest foot, the lighthouse is 376 feet away from the lighthouse.