a) y = -3
b) y = 2
c) y = 0
d) y = 2
Step-by-step explanation:
The asymptote is the constant added to the expression of the variable
a) y = 2^x - 3
Theexpression of the variable = 2^x
The number after it is is - 3
So the asymptote is y = -3
b) y = (1/3)^x + 2
The number added to the expression of the variable is 2
Asymptote is y = 2
c) y = 2(3)^x
y = 2(3)^x + 0
The expression of the variable = 2(3)^x
There is no number added to the expression of the variable
Hence, Asymptote is y = 0
d) 2 + 3^x
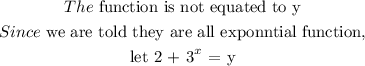
The expression of the variable = 3^x
The number added to this expression is 2
Asymptote is y = 2