Let:
x = biking speed
y = running speed
To solve this question, follow the steps below.
Step 01: Write an equation that relates the running and biking speed.
Given: His biking speed is 6 mph faster than his running speed
Then,
x = y + 6
Step 02: Write an equation to the total hours trained.
Given: speed = distance/time
Then, time = distance/speed
4 hours = (distance/speed)biking + ((distance/speed)running
Then,
4 = 15/x + 10/y
Step 03: Substitute x by (y + 6) in the equation from step 02.
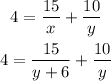
Step 04: Solve the equation above.
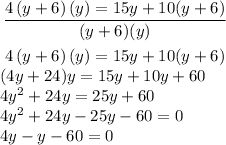
Use the quadratic formula to solve the equation. For a equation ax² + bx+ c = 0, the roots are:

Then, substituting the values from this question:
![\begin{gathered} y=(-b\pm√(b^2-4ac))/(2a) \\ y=(-(-1)\pm√((-1)^2-4*4*(-60)))/(2*4) \\ y=(1\pm√(1+960))/(8) \\ y=\frac{1\operatorname{\pm}√(961)}{8} \\ y=\frac{1\operatorname{\pm}31}{8} \\ y_1=(1-31)/(8)=-(30)/(8)=3.75 \\ y_2=(32)/(8)=4 \end{gathered}]()
Since y must be positive, y = 4 mph.
Step 06: Find x.
x = y + 6
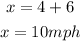
Since y = running speed:
Answer: the running speed was 4 mph.