Question

Right triangles and trigonometry special right triangles dont know the answers

Answer 1

In the given right triangle we are asked to determine the values of "x" and "y" given the 45 degrees angle. To do this we need to choose a trigonometric function that relates one of the unknown sides with a known side.

In a right triangle, if we are given an angle, then we can identify the following sides:

The hypotenuse is always the side that is in front of the 90 degrees angles (the angle identified with a square).

Given an angle, then its adjacent side is the side that is next to the angle.

The opposite side is the side in front of the given angle.

Following that system of sides, we have that in the given triangle the sides are:

Now that we have identified the sides of the given triangle we need to use a trigonometric function that relates the known sides with an unknown side.

Let's remember the definition of three basic trigonometric functions. The first function is sine:

`\sin \theta=(opposite)/(hypotenuse)`

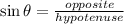
This means that the sine function is the quotient between the opposite sides and the hypotenuse.

The cosine function is defined as follows:

`\cos \theta=\frac{adjacent\text{ }}{hypotenuse}`

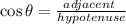
Therefore, the cosine function is the quotient between the adjacent side and the hypotenuse.

The tangent function is defined as:

`\tan \theta=(opposite)/(adjacent)`

Therefore, the tangent function is the quotient between the opposite side and the adjacent side.

The known side, in this case, is the hypotenuse (the side in front of the 90 degrees angle).

Side "x" is the adjacent side. A function that relates the adjacent side and the hypotenuse is cosine:

`\text{cos}45=\frac{adjacent}{\text{hypotenuse}}`

substituting the values of the sides we get:

`\cos 45=\frac{x}{10\sqrt[]{2}}`

Now we solve for "x" by multiplying both sides by the denominator:

`10\sqrt[]{2}\cos 45=x`

Now, the cos45 is equal to:

`\cos 45=\frac{1}{\sqrt[]{2}}`

Substituting this value we get:

`10\sqrt[]{2}(\frac{1}{\sqrt[]{2}})=x`

We can cancel out the square root of 2 and we get:

`10=x`

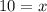
Therefore, the value of "x" is 10.

Now, to determine the value of "y" we need to have into account that "y" is the opposite sides, and the function that relates the opposite sides with the hypotenuse is sine, therefore, we have:

`\sin 45=(opposite)/(hypotenuse)`

Substituting the values of the sides:

`\sin 45=\frac{y}{10\sqrt[]{2}}`

Now we multiply both sides by the denominator and we get:

`10\sqrt[]{2}\sin 45=y`

The value of the sine of 45 is:

`\sin 45=\frac{1}{\sqrt[]{2}}`

Substituting these values we get:

`10\sqrt[]{2}(\frac{1}{\sqrt[]{2}})=y`

We can cancel out the square root of 2 and we get:

`10=y`

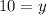
Therefore, y = 10.