Given:
Vertex: (-3, 3)
Focus: (-3, 2)
Let's find the distance from the point (x, y) to the focus of the parabola and the directrix.
To find the distance, apply the distance formula:
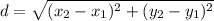
Thus, we have:
Distance from (x, y) to the focus:
Where:
(x1, y1) ==> (x, y)
(x2, y2) ==> (-3, 2)
Thus, we have:
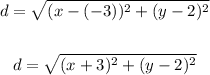
Therefore, the distance from the point (x, y) to the focus is:
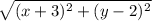
• The distance from the point to the directrix.
From the graph, the directrix is:
y = 4
Now, to find the distance, subtract the y-coordinate of the point from y = 4.
The distance is the absolute value of the result.
Thus, we have:

ANSWER:
Distance from the point to the focus:
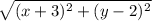
Distance from the point to directrix:
