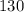Question

Section 2.4 question: 2 Suppose 27 blackberry plants started growing in a yard. Absent constraint, the blackberry plants will spread by 80% a month. If the yard can only sustain 140 plants, use a logistic growth model to estimate the number of plants after 5 months. plants

Answer 1

The question indicates that we should use a logistic model.

This can be given as

`P(t)=(K)/(1+Ae^(-kt));A=(K-P_o)/(P_0)`

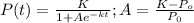
In this case. K is the carrying capacity =140

Po is the initial population=27

`\begin{gathered} \therefore A=(140-27)/(27) \\ A=4.185 \end{gathered}`

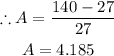
This then brings the model to be

`P(t)=(140)/(1+4.185e^(-kt))`

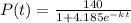
The next step would be to find the value of k

Since the blackberry plants increase by 80% every month. Therefore, for 1 month we would have

`27+(80)/(100)*27=48.6`

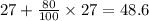
This implies that for that first month we would have

`\begin{gathered} (140)/(1+4.185e^(-k*1))=48.6 \\ (140)/(1+4.185e^(-k))=48.6 \\ 140=48.6+203.391e^(-k) \\ 91.4=203.391e^(-k) \\ e^(-k)=(91.4)/(203.391) \\ e^(-k)=0.44938 \\ \ln (e^(-k))=\ln 0.44938 \\ -k=-0.7999 \\ k=0.7999 \end{gathered}`

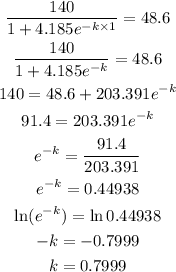
Therefore for 5 months, we would have

`\begin{gathered} P(5)=(140)/(1+4.185e^(-0.7999*5)) \\ P(5)=(140)/(1+4.185e^(-3.9995)) \\ P(5)=(140)/(1.0770352) \\ P(5)=129.986\approx130 \end{gathered}`

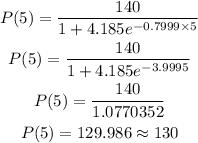
Answer: Using the logistic model the estimated number of plants after 5 months becomes

`130`