Answer:
0.08
Step-by-step explanation:
We can represent the situation with the following figure
Now, by the conservation of energy, we can write the following equation
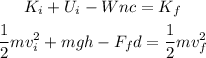
Where m is the mass, vi is the initial velocity, g is the gravity, h is the height, Ff is the force of friction, d is the distance traveled by the sledge, and vf is the final velocity.
Using the free body diagram, we get that the force of friction is equal to
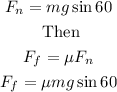
Now, we can replace the expression for Ff in the equation above and solve for the coefficient of friction μ
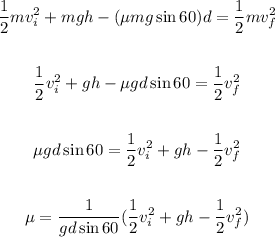
Replacing g = 9.8 m/s², d = 16 m, vi = 3 m/s, h = 8 m, and vf = 12 m/s, we get
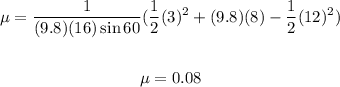
Therefore, the coefficient of friction is 0.08