Given a polynomial of the following form:
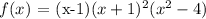
Equaling f(x) to zero:
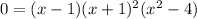
If we know that f(x) is equal to zero, then at least one term or all terms are equal to zero.
Equaling each term to zero as shown as follows:
x-1 = 0 (x+1)^2 = 0 x^2-4 = 0
Isolating the x:
x=1 x=-1 x=± 2
Now, looking at the degree of the power of each term.
(x-1)^1 --> m=1 [odd] (x+1)^2--> m=2 [even] (x^2-4)^1-->m=1 [odd]
Now, we can draw the graph: