Question

Consider the functions below. Match each with its simplified form.

Answer 1

We are given the following functions:

`\begin{gathered} P(x)=(2)/(3x-1) \\ \\ Q(x)=(6)/(-3x+2) \end{gathered}`

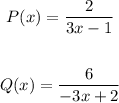
We are asked to determine:

`P(x)/ Q(x)`

This is equivalent to:

`(P(x))/(Q(x))`

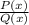
Substituting the functions:

`(P(x))/(Q(x))=((2)/(3x-1))/((6)/(-3x+2))`

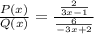
Now, we use the following property:

`((a)/(b))/((c)/(d))=(a)/(b)*(d)/(c)`

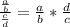
Applying the property we get:

`(P(x))/(Q(x))=((2)/(3x-1))((-3x+2)/(6))`

Solving the products:

`(P(x))/(Q(x))=(2(-3x+2))/(6(3x-1))`

Simplifying we get:

`(P(x))/(Q(x))=(-3x+2)/(3(3x-1))`

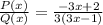
And thus we get the desired expression.

Now, we are asked to determine:

`P(x)*Q(x)`

This is the product of the functions. Substituting we get:

`P(x)*Q(x)=((2)/(3x-1))((6)/(-3x+2))`

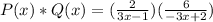
Solving the products:

`P(x)*Q(x)=(12)/((3x-1)(-3x+2))`

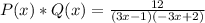
Since we can't simplify any further this is the final answer.