Question

Operations with Radical Expressions I’m still learning about this concept and I’m having trouble understanding the complexity of the problem!

Answer 1

Step-by-step explanation:

Question 3.

Before we simplify the radical expression let us note the following.

`\begin{gathered} 27=9*3 \\ 45=9*5 \end{gathered}`

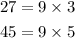
Therefore, we can write our radical function as

`\begin{gathered} -\sqrt[]{27}-2\sqrt[]{27}+2\sqrt[]{45} \\ \Rightarrow-\sqrt[]{9*3}-2\sqrt[]{9*3}+2\sqrt[]{9*5} \end{gathered}`

Now,

`\begin{gathered} \sqrt[]{9*3}=\sqrt[]{9}*\sqrt[]{3}=3\sqrt[]{3} \\ \sqrt[]{9*5}=\sqrt[]{9}*\sqrt[]{5}=3\sqrt[]{5} \end{gathered}`

therefore, our expression becomes

`\begin{gathered} -\sqrt[]{9*3}-2\sqrt[]{9*3}+2\sqrt[]{9*5} \\ \Rightarrow-3\sqrt[]{3}-2(3\sqrt[]{3})+2(3\sqrt[]{5}) \end{gathered}`

which simplifies to give

`-3\sqrt[]{3}-6\sqrt[]{3}+6\sqrt[]{5}`

since -3√3 - 6 √3 = - 9 √3 ( just add them up), the above becomes

`-9\sqrt[]{3}+6\sqrt[]{5}`

We cannot simplify the above function any further. Therefore, the above expression is our final answer.

Question 5.

Since -3√ 27 - 3√27 = -6 √27, our expression becomes

`-3\sqrt[]{20}-6\sqrt[]{27}`

Let us also note that

`\begin{gathered} 20=4*5 \\ 27=3*9 \end{gathered}`

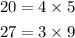
therefore,

`\begin{gathered} \sqrt[]{27}=\sqrt[]{3*9} \\ \sqrt[]{20}=\sqrt[]{4*5} \end{gathered}`

therefore, our expression becomes

`-3\sqrt[]{4*5}-6\sqrt[]{3*9}`

Now since

`\begin{gathered} \sqrt[]{4*5}=\sqrt[]{4}*\sqrt[]{5}=2\sqrt[]{5} \\ \sqrt[]{3*9}=\sqrt[]{3}*\sqrt[]{9}=3\sqrt[]{3} \end{gathered}`

the above becomes

`-3(2\sqrt[]{5})-6(3\sqrt[]{3})`
`\Rightarrow-6\sqrt[]{5}-18\sqrt[]{3}`

We cannot simplify the above function any further. Therefore, the above expression is our final answer.