Question

Writing Solve the system using addition. Use pencil and paper. Explain why the addition method is agood choice for solving the system. If you wanted to solve for x first, is the addition method still a goodchoice? Explain.X-3.3y = 5.6- X+4.9y = -8.8

Answer 1

Given the two equations

`\begin{gathered} x-3.3y=5.6 \\ -x+4.9y=-8.8 \end{gathered}`

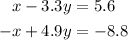
If we have to solve this question, we will do so easily using the addition method because we can easily eliminate x. Also because we will avoid using fractions to get our answers

Thus if we add the two equations

`\begin{gathered} -3.3y+4.9y=5.6-8.8 \\ 1.6y=-3.2 \\ y=-2 \end{gathered}`

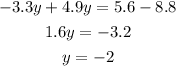
Then, the value of x from the first equation

`\begin{gathered} x-3.3y=5.6 \\ x-3.3(-2)=5.6 \\ x+6.6=5.6 \\ x=5.6-6.6 \\ x=-1 \end{gathered}`

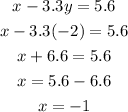
Therefore

`x=-1,y=-2`

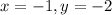
If we wanted to solve for x first, this method of addition would not be convenient because the coefficients of y in the two equations are neither the same nor equal to one.