Question

if the number of home runs in a league are normally distributed and have a mean of 94 and a standard deviation of 8, what percentage of the teams have scored more than 102 home runs?

Answer 1

To start, we need to find the z-score for 102, by using the following formula:

`\begin{gathered} z=(x-\mu)/(\sigma) \\ \text{where} \\ z\text{ is the z-score} \\ x\text{ is the value we are evaluating 102} \\ \mu\text{ is the mean 94} \\ \sigma\text{ is the standard deviation 8} \end{gathered}`

By replacing the know values, we obtain the z-score:

`\begin{gathered} z=(102-94)/(8) \\ z=(8)/(8) \\ z=1 \end{gathered}`

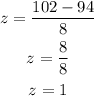
Thus, the probability of x>102 is equal to 1-P(z<1), and this one we can find it in a standard normal table:

`\begin{gathered} P(x>120)=1-P(z<1) \\ P(x>120)=1-0.8413 \\ P(x>120)=0.1587 \end{gathered}`

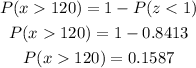
The probability is 0.1587*100%=15.87%

Answer: 15.87% of the teams have scored more than 102 home runs