1 Answer

Tylisha · Answer 1 · 2023-03-22T12:45:04+0000

ANSWER:

189.52 kg*m^2

Explanation:

Given:

mr = 8 kg

ms = 36.25 kg

L = 6 m

R = 1.5 m

Moment of inertia of rod about its center of mass:

$I_{\operatorname{cm}}=(1)/(12)\cdot m_r\cdot L^2$

Parallel axis theorem for the rod gives:

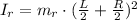
$I_r=m_r\cdot((L)/(2)+(R)/(2))^2$

Paraller axis theorem for the spehere gives:

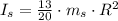
$I_s=(13)/(20)\cdot m_s\cdot R^2$

Therefore:

$\begin{gathered} I=I_{\operatorname{cm}}+I_r+I_s \\ I=(1)/(12)m_rL^2+m_r((L)/(2)+(R)/(2))^2+(13)/(20)m_sR^2 \end{gathered}$

Replacing:

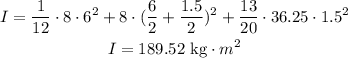
$\begin{gathered} I=(1)/(12)\cdot8\cdot6^2+8\cdot((6)/(2)+(1.5)/(2))^2+(13)/(20)\cdot36.25\cdot1.5^2 \\ I=189.52\text{ kg}\cdot m^2 \end{gathered}$

The moment of inertia is 189.52 kg*m^2

Please log in or register to add a comment.