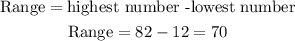The given data set is:
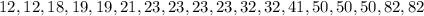
a) The Mean:
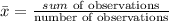
Thus,
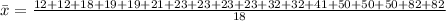
![\begin{gathered} \bar{x=(612)/(18)} \\ \operatorname{mean}=34 \end{gathered}]()
b) The median;
The median is the middle number or the average of the numbers if there are two(2) middle numbers.
However, the observations have to be arranged in ascending order.
In this case, the observations are already arranged from the lowest to the highest.
Thus, we have:
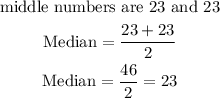
c) The Mode;
The mode is the most occuring observation.
Thus, the Mode is 4
d) The Range: