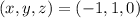GIVEN
A parallelogram ABCD with given vertices
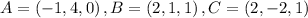
SOLUTION
Let the fourth vertex D have coordinates (x, y, z).
The diagonals of a parallelogram bisect each other. Therefore, the midpoint of the two diagonals must coincide.
For a parallelogram ABCD, the diagonals are AC and BD.
Recall the midpoint formula:
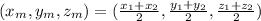
Therefore, the midpoint for AC will be:
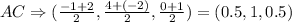
The midpoint of BD will be:
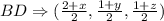
Equate the midpoints:
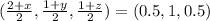
Therefore:
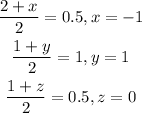
Therefore, the coordinates of the fourth vertex will be: