Given the ratio:
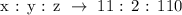
To be able to get the value of y at x = 13 and z = 195, let's recall how this ratio transforms into an equation:
At x : y : z
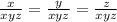
Let's now plugin the values to be able to find the value of y:
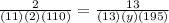
Let's simplify the equation:
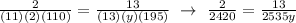
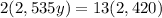
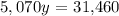
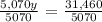
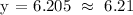
Therefore, y = 6.21