We have a triangle with 2 sides of length 15 and 19.
We have to find the smallest possible whole number length for the 3rd side.
We can draw this as:
The third size is x.
If we reduce h, approaching to 0, x is minimized.
When h is very close to 0 (if h=0, the triangle cease to exist), the value of x can be written as a little bigger than the difference between the largest side (19) and the other side (15).
Then, x is, in the limit h-->0:
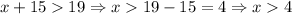
As x>4, the next whole number is 5.
NOTE: if x=4, the triangle does not exist, as there is no height or 3 angles.
Answer: The smallest whole number length for the 3rd side is 5.