Given:
• Mass of each, m = 1.67 x 10⁻²⁷ kg
,
• Velocity, v = 9.26 x 10⁶ m/s
,
• B = 2.84 teslas
Let's sole for the following:
• (a). What magnetic force acts on the alpha particle?
Apply the formula:
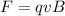
Where:
Charge of proton = 1.609 x 10⁻¹⁹ C
Charge of neutron = 0
Thus, we have:
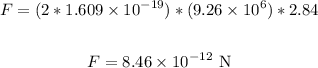
The magnetic force that acts on the alpha particle is 8.46 x 10⁻¹² N.
• (b). Let's find the radius of curvature of the path of the alpha particle?
To find the radius, apply the formula:
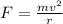
Where:
F is the force
m is the total mass
v is the velocity
r is the radius
Rewrite the formula for r, plug in the values and solve.
We have:
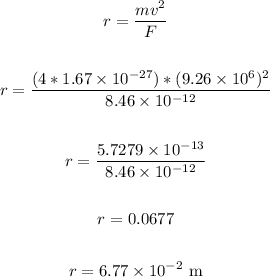
The radius of the curvature of the path is 6.77 x 10⁻² m.
ANSWER:
(a). 8.46 x 10⁻¹² N.
(b). 6.77 x 10⁻² m.