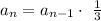ANSWER
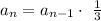
Step-by-step explanation
We want to write the recursive definition of the situation represented in the table.
The original area of the paper is 81 cm² and with each strip that is cut off, we are left with 1/3 of the area of the former paper.
We can therefore, say that this situation represents a geometric progression, where the value of the next term can be gotten by multiplying a constant factor to the former term.
The general recursive definition of a geometric progression is given as:

The common ratio is the factor that multiplies each term, as described earlier.
From the question, the common ratio is 1/3, since each new strip is 1/3 the area of the former strip.
Therefore, the recursive definition of the data in the table is: