Question

I eill drop a picture

Answer 1

Parallel lines have the same slope, that is

`\begin{gathered} m_1=m_2_{} \\ \text{ Where} \\ m_1\text{ is the slope of line 1 and} \\ m_2\text{ is the slope of line 2} \end{gathered}`

The slope of line 1 is 1/3 because its equation is written in slope-intercept form, that is

`\begin{gathered} y=mx+b \\ \text{ Where m is the slope and} \\ \text{b is the y-intercept} \\ y=(1)/(3)x-1\Rightarrow\text{ Line 1} \\ m_1=(1)/(3)\Rightarrow\text{ Slope of the line 1} \end{gathered}`

Now, since the slopes are parallel then you already have the slope of line 2:

`\begin{gathered} m_1=m_2 \\ (1)/(3)=m_2 \end{gathered}`

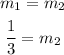
Then, you can use the point-slope equation to find the equation for line 2:

`\begin{gathered} y-y_1=m(x-x_1)\Rightarrow\text{ Point-slope equation} \\ \text{ Where m is the slope and} \\ (x_1,y_1)\text{ is a point through which the line passes} \end{gathered}`

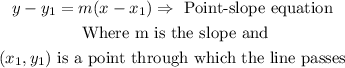
So, you have

`\begin{gathered} m_2=(1)/(3) \\ (x_1,y_1)=(6,10) \\ y-y_1=m(x-x_1) \\ y-10=(1)/(3)(x-6) \end{gathered}`

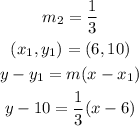
Finally, to obtain the equation of the line in its slope-intercept form, solve for y:

`\begin{gathered} y-10=(1)/(3)(x-6) \\ \text{ Apply the distributive property to the right side of the equation} \\ y-10=(1)/(3)x-(1)/(3)\cdot6 \\ y-10=(1)/(3)x-2 \\ \text{ Add 10 from both sides of the equation} \\ y-10+10=(1)/(3)x-2+10 \\ y=(1)/(3)x+8 \end{gathered}`

Therefore, the equation in slope-intercept form of the line that passes through (6,10) and is parallel to the given equation is

`y=(1)/(3)x+8`

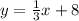
and the correct answer is option A.