Question

51) Write the equation of the line passing through (-2, 5) and perpendicular x + 3y = 15.

Answer 1

The genral equation of straight line is y=mx+c, where m is the slope of the line and c is the y intercept.

The given line is x+3y=15. Rewrite this equation in the form y=mx+c.

`\begin{gathered} x+3y=15 \\ 3y=-x+15 \\ y=(-1)/(3)x+(15)/(3) \\ y=(-1)/(3)x+5 \end{gathered}`

Comparing above equation with y=mx+c, we can write

`\text{Slope, m=}(-1)/(3)`

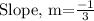
The slope of a line perpendicular to x+3y=15 is the negative reciprocal of the slope m. Hence, the slope of the perpendicular line can be written as,

`m_1=-(1)/(m)=-((1)/((-1)/(3)))=3`

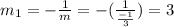
Let (x1,y1)=( -2,5). Now, the equation of the line with slope m1 and passing through (x1,y1) can be written as,

`\begin{gathered} m_1=(y_1-y)/(x_1-x) \\ 3=(5-y)/(-2-x) \\ 3(-2-x)=5-y \\ -6-3x=5-y \\ y=3x+11 \end{gathered}`

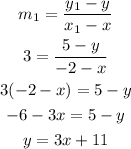
Theefore, the equation of aline passing through (-2,5) and perpendicular to x+3y=15 is y=3x+11.