The question involves a direct variation between x and y,therefore
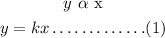
Given that,
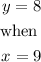
Substitute the values of x and y in equation (1)
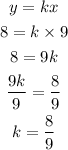
Substituting the value of k=8/9 in equation (1), we will have the equation of variation to be
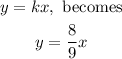
Hence,
The equation of the variation is y= 8x/9
Next, we will calculate the value of y when x=72 using the equation of variation above
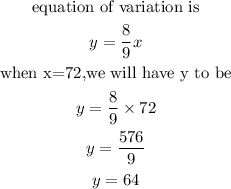
Hence,
The value of y when x=72 is y=64