Question

Suppose that your income is $34,300 per year and you receive a cost-of-living raise each year. If inflation is constant at 10.6 % annually, in how many years will you bemaking $42,700 per year? Round your answer to the nearest whole number.

Answer 1

In order to calculate how many years it will take, we can use the formula for compound interest:

`A=P\cdot(1+i)^t`

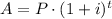
Where A is the final amount after t years, P is the principal (initial amount) and i is the annual interest.

So, using A = 42700, P = 34300 and i = 0.106, we have:

`\begin{gathered} 42700=34300(1+0.106)^t \\ (42700)/(34300)=1.106^t \\ 1.106^t=1.2449 \\ \ln (1.106^t)=\ln (1.2449) \\ t\cdot\ln (1.106)=\ln (1.2449) \\ t\cdot0.10075=0.219055 \\ t=(0.219055)/(0.10075)=2.1742 \end{gathered}`

Rounding to the nearest whole number, it will take 2 years.