Given the system of equations:
• 6x - 2y = 36
,
• -3x + 3y = 12
The solution:
(x, y) ==> (11, 15)
Let's determine whether the given ordered pair is a solution to the system of equations.
Let's solve the system using the addition and elimination method.
Multiply both equations so the coefficients of one variable are opposite.
Multiply equation 2 by 2:
6x - 2y = 36
2(-3x + 3y) = 2(12)
• 6x - 2y = 36
,
• -6x + 6y = 24
Add both equations:
6x - 2y = 36
-6x + 6y = 24
____________
0 + 4y = 60
We now have:
4y = 60
Divide both sides by 4:
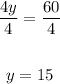
Plug in 15 for y in either of the equations.
Take the first equation:
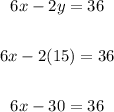
Add 30 to both sides:

Divide both sides by 6:

Therefore, the solution is:
x = 11, y = 15
In point form, the solution is: (11, 15)
Therefore, the given ordered pair is a solution to the system of equations.
ANSWER:
Yes, the ordered pair is a solution to the system of equations.