The standard sine function is given by:
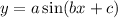
Where:
Amplitude = 2a
Period = 2π/b
Horizontal shift = c
In this case, we have:
- Maximum of 6 and minimum of negative 6, hence the amplitude is 12, this is
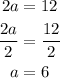
- The period is 2π/3, therefore:
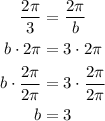
- The graph passes through the y-axis at (0,2), which is 1/3 of the maximum. Considering the shift, we have

Answer:
a = 6, b = 3, c = π