Step 1: Write out the coordinate of the midpoint
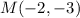
Step 2: Find the coordinates of the two line segments by testing for values that will yeild the midpoint coordinates
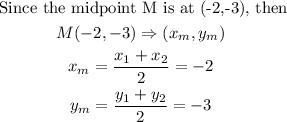
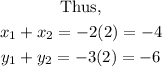
From the above, we can deduce to four values that will give -4 for the x-values and -6 for the y-values.
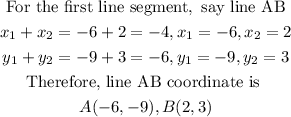
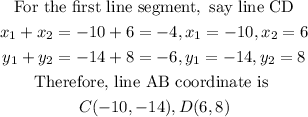
Step 3: Draw the two lines segment on a cartesian plane showing M as the common midpoint.