Question

Area involving rectangles and circlesEspañolVA training field is formed by joining a rectangle and two semicircles, as shown below. The rectangle is 82 m long and 64 m wide.Find the area of the training field. Use the value 3.14 for , and do not round your answer. Be sure to include the correct unit in your answer.

Answer 1

8463.36 m^2

Step-by-step explanation:

Given the length(l) of the rectangle as 82m and the width(w) as 64m, we can go ahead and determine the area of the rectangle as follows;

`\begin{gathered} \text{Area of a rectangle }=l* b \\ =82*64 \\ =5248m^2 \end{gathered}`

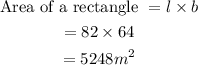
The two semi-circles are equivalent to one circle with a diameter of 64m, so the radius of the circle will be;

`\text{Radius(r)}=(Diameter(d))/(2)=(64)/(2)=32m`

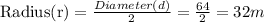
Let's go ahead and determine the area of the circle given pi as 3.14;

`\begin{gathered} Area\text{ of a circle=}\pi* r^2 \\ =3.14*(32)^2 \\ =3.14*1024 \\ =3215.36m^2 \end{gathered}`

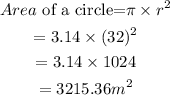
Therefore, the area of the training field can be determined by adding the area of the rectangle and that of the two semicircles;

`\begin{gathered} \text{Area of the training field}=\text{Area of rectangle + Area of two semicircles} \\ =5248+3215.36 \\ =8463.36m^2 \end{gathered}`