The formula to calculate the total interest paid is:
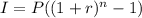
Where:
• I, is the total interest paid
,
• P, is the amount borrowed
,
• r, is the interest rate
,
• n, is the times that the interest was compounded
Solving this formula for P,
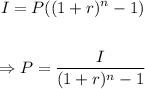
Using the data given,
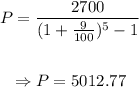
Therefore, we can conclude that he borrowed $5,012.77