Equation of the line
There are several forms to express the equation of a line.
The equation of the line in slope-intercept form is:
y=mx+b
Being m the slope and b the y-intercept.
The equation of a line passing through points (x1,y1) and (x2,y2) can be found as follows:
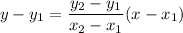
The standard form of a line is:
Ax + By = C
We are given two points (1,2) and (3,10). The point-point equation is adequate according to the data we are provided.
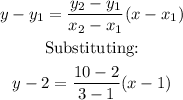
Operating:
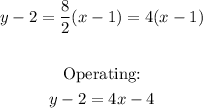
Subtracting 4x and adding 2:
y - 4x = -4 + 2 = -2
Rearranging:
-4x + y = -2
This is the required equation in standard form