Question

asked Mar 12, 2023 37.2k views

1 Answer

Robin Curbelo · Answer 1 · 2023-03-17T10:38:40+0000

We will have to find the equation that follows the form:

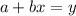
That is:

*The value of a is:

*The value of b is:

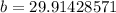
So, the linear regression is:

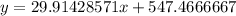
We can see it graphically as follows:

Here we can see the linear regression line and the points used.

***How to manually determine linear regressions***

We will start as follows:

We will have to use the following expressions in order to manually find the linear regression:

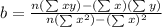
$b=\frac{n(\sum^{}_{}xy)-(\sum^{}_{}x)(\sum^{}_{}y)}{n(\sum^{}_{}x^2)-(\sum^{}_{}x)^2}$

And:

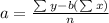
$a=\frac{\sum ^{}_{}y-b(\sum ^{}_{}x)}{n}$

Here we have that n is the number of values on the dataset. So, we solve for b as follows [Based on the problem given]:

*We will determine the values of n, the sum of x, the sum of y, xy, x^2 & y^2 as follows:

Sum of x:

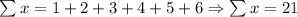
$\sum ^{}_{}x=1+2+3+4+5+6\Rightarrow\sum ^{}_{}x=21$

Sum of y:

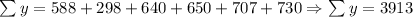
$\sum ^{}_{}y=588+298+640+650+707+730\Rightarrow\sum ^{}_{}y=3913$

Value of n: We have that the number of datasets given is 6 [6 pairs of values on the table].

*The sum of xy:

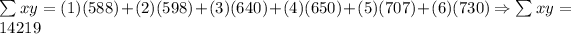
$\sum ^{}_{}xy=(1)(588)+(2)(598)+(3)(640)+(4)(650)+(5)(707)+(6)(730)\Rightarrow\sum ^{}_{}xy=14219$

*The sum of X^2:

$\sum ^{}_{}x^2=1^2+2^2+3^2+4^2+5^2+6^2\Rightarrow\sum ^{}_{}x^2=91$

*The square of the sum of x:

$(\sum ^{}_{}x)^2=21^2\Rightarrow(\sum ^{}_{}x)^2=441$

Now that we have all the values, we replace in the first equation and solve for b:

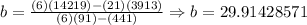
$b=((6)(14219)-(21)(3913))/((6)(91)-(441))\Rightarrow b=29.91428571$

And we solve now for a:

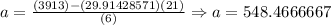
$a=((3913)-(29.91428571)(21))/((6))\Rightarrow a=548.4666667$

And then we simply replace on the expression:

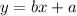
And the expression after the replacement of a & b is the linear regression.

Please log in or register to add a comment.