Hello there. To solve this question, we'll have to remember some properties about dividing polynomials.
Given the polynomials, we want to evaluate the division:
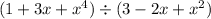
Rewriting it the way we perform long division:
We start with the higher degree terms, namely x^4 and x².
Dividing x^4 by x², we get x². Now we multiply every term from the division by this factor and subtract from the term being divided.
Now, we have a 2x³ as the higher degree term from the term being divided. Dividing it by x², we get 2x. Multiply each term of the divisor and subtract from it.
Finally, the highest degree term from the term being divided is x². Dividing it by x², we get 1. Multiply each term of the divisor and subtract it from the dividend.
Now, the highest degree term from the dividend is -x, when the highest degree term from the divisor is x². We cannot proceed with the long division anymore.
It means that we have a quotient:
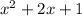
And a remainder:
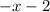
Notice if we rewrite it as:
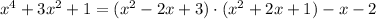
We have the division P(x)/D(x) written in the form:
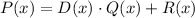
Where Q(x) and R(x) are the quotient and remainder polynomials.