Answer:
4.6 mm
Step-by-step explanation:
The Young's Modulus is defined as
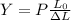
Where
Y = Young's Modulus
P = pressure (stress) applied
L0 = inital length
ΔL = change in length
Now in our case, we know that the femur is 0.49 m long (L0 = 0.49) and it can withstand max stress of 1.69 x 10^8 Pa ( P = 1.69 x 10^8 Pa), and Young's Modulus for the bone is 1.8 x 10^10 Pa ( Y = 1.8 x 10^10 Pa ); therefore, the above formula gives
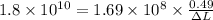
We have to solve the above equation for ΔL, the amount of compression.
Multiplying both sides by ΔL gives
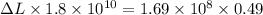
dividing both sides by 1.8 x 10^10 gives
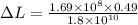
which we evaluate to get
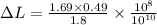
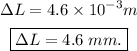
Hence, the amount of compression a femur can withstand is 4.6 x 10^-3 m or 4.6 mm.