A satellite is in orbit 600 km above Earth's surface. Earth's radius is about 6370 km. Using the Pythagorean Theorem, the distance (x) from the satellite to Earth'…

Question

asked Jul 27, 2023 134k views

1 Answer

Jose Leon · Answer 1 · 2023-08-02T19:15:50+0000

Answer:

2829.13 km.

Step-by-step explanation:

If the radius of the Earth is 6370 km, the distance of the segment CD is also 6370 km.

Then, the sides of the rigth triangle are:

CB = 6370 km

AC = AD + DC

AC = 600 km + 6370 km

AC = 6970 km

AB = x

So, using the Pythagorean theorem we can calculate the value of x as follows:

$\begin{gathered} AB=\sqrt[]{(AC)^2-(CB)^2} \\ x=\sqrt[\square]{6970^2-6370^2} \end{gathered}$

Because AC is the hypotenuse and CB is on the legs of the triangle.

Therefore, solving for x, we get:

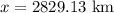
$x=2829.13\text{ km}$

Then, the answer is:

The distance (x) from the satellite to Earth's horizon is 2829.13 km.