ANSWER
C. x² - x ≥ 6
Step-by-step explanation
Let's analyze the solution set graphed first. We can see that the values -2 and 3 are included in the set, and all values below -2 and above 3. So, the solution set is (-∞, 2] U [3, ∞).
To find which inequality satisfies this solution set we have to solve them. To do so, we will be using the quadratic formula:

A. To solve this one, first, add x to both sides,
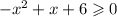
Now, apply the quadratic formula to find the zeros. For this inequality, a = -1, b = 1, and c = 6
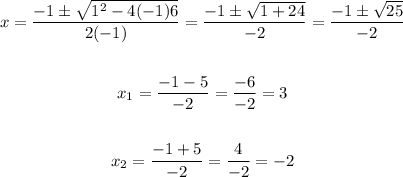
But in this case, the solution set is [-2, 3] - note that for any value outside this interval the inequality is false.
B. Similarly, apply the quadratic formula for a = -3, b = 3, c = 18,
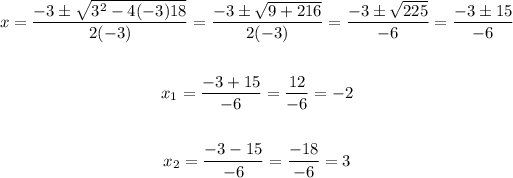
Again, the solution set is [-2, 3] since for any value outside the interval the inequality is not true.
C. Subtract 6 from both sides,
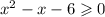
Apply the quadratic formula, with a = 1, b = -1, and c = -6,
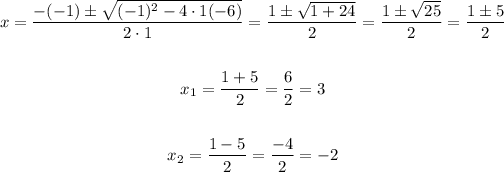
In this case, if we take any value between -2 and 3, for example 1,

We can see that the inequality is false, while if we take a value greater than 3 or less than -2, for example, -5,
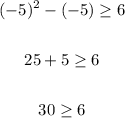
We can see that the inequality is true.
Hence, we can conclude that inequality C satisfies the solution set graphed.